Отклонением расположении называется отклонение реального расположения рассматриваемого элемента от его номинального расположения. Под номинальным понимается расположение, определяемое номинальными линейными и угловыми размерами между рассматриваемым элементом и базами. Номинальное расположение определяется непосредственно изображением детали на чертеже без числового значения номинального размера между элементами, когда:

• - номинальный линейный размер равен нулю (требования соосности, симметричности, совмещения элементов в одной плоскости);
• - номинальный угловой размер равен 0 или 180° (требование параллельности);
• - номинальный угловой размер равен 90° (требование перпендикулярности).

В табл. 5.40 приведены отклонения, относящиеся к группе отклонении и допуски расположении поверхностей.

При определении номинального расположения плоских поверхностей координирующие размеры задают непосредственно от баз. Для поверхностей тел вращения и других симметричных групп поверхностей координирующие размеры обычно задают от их осей или плоскостей симметрии.

Для оценки точности расположения поверхностей, как правило, назначают базы.

База - элемент детали (или выполняющие ту же функцию сочетания элементов), определяющий одну из плоскостей или осей координат, по отношению к которой задается допуск расположения или определяется отклонение расположения рассматриваемого элемента.

Базами могут быть, например, базовая плоскость, базовая ось, базовая плоскость симметрии. В качестве базовой оси в зависимости от требований может быть задана ось базовой поверхности вращения или общая ось двух или нескольких поверхностей вращения. В качестве базовой плоскости симметрии может быть задана плоскость симметрии базового элемента или общая плоскость симметрии двух или нескольких элементов. Примеры обшей оси и обшей плоскости симметрии нескольких элементов приведены в табл. 5.41.

Иногда для однозначной оценки точности расположения отдельных элементов деталь должна быть ориентирована одновременно по двум или трем базам, образующим систему координат, по отношению к которой задается допуск расположения или определяется отклонение расположения рассматриваемого элемента. Такая совокупность баз называется комплектом баз.

Базы, образующие комплект баз, различают в порядке убывания числа степеней свободы, лишаемых ими (рис. 5.53): база Л

Рис. 5.53.

А - установочная база; В - направляющая база; С - опорная база

лишает деталь трех степеней свободы (называется установочной базой), база В - двух (называется направляющей базой), а база С - одной степени свободы (называется опорной базой).

Максимальная точность достигается в том случае, когда соблюден "принцип единства баз", т. е. конструкторские базы совпадают с технологическими и измерительными базами.

Если базы не заданы или задан комплект баз, лишающий деталь менее чем шести степеней свободы, то расположение системы координат, в которой задан допуск расположения данного элемента относительно других элементов детали, ограничивается по оставшимся степеням свободы лишь условием соблюдения заданного допуска расположения, а при измерении - условием получения минимального значения отклонения.

Допуском расположения называется предел, ограничивающий допускаемое значение отклонение расположения поверхностей.

Поле допуска расположения - это область в пространстве или заданной плоскости, внутри которой должен находиться прилегающий элемент или ось, центр, плоскость симметрии в пределах нормируемого участка. Ширина или диаметр поля допуска определяется значением допуска, а расположение относительно баз определяется номинальным расположением рассматриваемого элемента.

Рассмотрим основные виды отклонений расположения поверхностей.

Отклонение от параллельности плоскостей - разность Д наибольшего а и наименьшего Ь расстояний между плоскостями в пределах нормируемого участка £" т. е. Д = а - Ь (рис. 5.54, а). Поле допуска параллельности плоскостей определяет область в пространстве, ограниченную двумя параллельными плоскостями, отстоящими друг от друга на расстоянии, равном допуску параллельности Г, и параллельными базовой плоскости (рис. 5.54, б). Примеры обозначения на чертеже приведены на рис. 5.54, в и г. допуск параллельности поверхности Б относительно поверхности Л 0,01 мм (рис. 5.54, в); допуск параллельности поверхности Ли БОА мм (рис. 5.54, г).

В обоснованных случаях могут нормироваться суммарные отклонения формы и расположения поверхностей или профилей.

Суммарное отклонение от параллельности и плоскости - разность Д наибольшего а и наименьшего Ь расстояний от точек реальной поверхности до базовой плоскости в пределах нормируемого участка Ь19 т. е. Д = а - Ь (рис. 5.84, д). Поле суммарного допуска

Рис. 5.54.

параллельности и плоскостности - область в пространстве, ограниченная двумя параллельными плоскостями, отстоящими друг от друга на расстоянии, равном суммарному допуску параллельности и плоскостности Ти параллельными базовой плоскости (рис. 5.54, е). Примеры обозначения на чертеже: суммарный допуск параллельности и плоскостности поверхности ^относительно поверхности А 0,01 мм (рис. 5.54, ж).

Отклонение от параллельности оси относительно плоскости или плоскости относительно оси - разность Д наибольшего а и наименьшего Ь расстояний между осью и плоскостью на длине нормируемого участка I (рис. 5.55, а).

Рис. 5.55.

Допуск параллельности оси относительно плоскости Т покатан на рис.5.55, б, а допуск параллельности плоскости относительно оси Т- на рис.5.55, в. Примеры условного обозначения на чертеже: допуск параллельности оси отверстия относительно поверхности А 0,01 мм (рис. 5.55, г); допуск параллельности обшей оси отверстий относительно поверхности А 0,01 мм (рис. 5.55, д) допуск параллельности поверхности Б относительно оси поверхности А 0,01 мм (рис. 5.55, е).

Отклонении от параллельности прямых в плоскости - разность Д наибольшего а и наименьшего Ь расстояний между прямыми на длине нормируемого участка, т. е. Д = а - Ь (рис. 5.55, ж). Графическое изображение допуска параллельности прямых в плоскости показано на рис.5.55, з.

Отклонение от параллельности осей или прямых в пространстве - это геометрическая сумма О отклонений от параллельности проекций осей (прямых) в двух взаимно перпендикулярных плоскостях; одна из этих плоскостей является обшей плоскостью осей - Ак = а - Ь

Д=^Д2Х+Д2Г (рис. 5.55, и). Поле допуска для случая, когда заданы

раздельно допуск параллельности осей в обшей плоскости (7"() и допуск (Г), покатано на рис. 5.55, к, а для случая, когда задан допуск Т параллельности осей в пространстве, - на рис. 5.56, б. Пример обозначения на чертеже: допуск параллельности оси отверстия А 0 0,01 мм (рис. 5.55, л).

Отклонение от параллельности осей (или прямых) в общей плоскости - отклонение от параллельности Д(проекций осей (прямых) на их общую плоскость (рис. 5.56, а).

Перекос осей (или прямых) - отклонение от параллельности Д(проекций осей на плоскость, перпендикулярную обшей плоскости осей и проходящую через одну из осей (базовую) (рис. 5.56, д).

Пример обозначения на чертеже: допуск параллельности оси отверстия Б относительно оси отверстия А 0,1 мм, допуск перекоса осей 0,25 мм (рис. 5.56, в, г).

Отклонение от перпендикулярности плоскостей - отклонение утла между плоскостями от прямого (90°), выраженное в линейных единицах Д на длине нормируемого участка (рис. 5.57, а). Графическое изображение допуска перпендикулярности плоскостей Т покатано на рис. 5.57, б. Условное обозначение на чертеже: допуск перпендикулярности поверхности Б относительно основания 0,1 мм (рис. 5.57, б).

Суммарное отклонение от перпендикулярности и плоскостности - разность д наибольшего и наименьшего расстояний от точек реальной поверхности до плоскости, перпендикулярной базовой плоскости или базовой оси в пределах нормируемого участка I (рис. 5.57, г).

Графическое изображение суммарного допуска перпендикулярности и плоскостности Т показано на рис. 5.57, д. Условное обозначение на чертеже: суммарный допуск перпендикулярности и плоскостности поверхности Б относительно поверхности А 0,2 мм (рис. 5.57, е).

Отклонение от перпендикулярности плоскости иди оси относительно оси - отклонение угла между плоскостью или осью и базовой осью от прямого утла (90°), выраженное в линейных единицах Д на длине нормируемого участка Ь (рис. 5.57, ж). Графическое изображение допуска перпендикулярности плоскости или оси относительно оси Т показано на рис. 5.57, з. Условное обозначение на чертеже: допуск перпендикулярности оси отверстия Б относительно поверхности А 0,04 мм (рис. 5.57, и).

Отклонение от перпендикулярности оси относительно плоскости - отклонение угла между осью и базовой плоскостью от прямого утла (90°), выраженное в линейных единицах Д на длине нормируемого участка Ь (рис. 5.57, к). Графическое изображение допуска перпендикулярности оси относительно плоскости показано на рис. 5.57, л, если допуск Т задан со знаком 0, и на рис. 5.57, ", если заданы допуски в двух взаимно перпендикулярных направлениях Т{ и Т2.

Условное обозначение на чертеже: допуск перпендикулярности оси отверстия Б относительно поверхности А 0 0,01 мм (рис. 5.57, л/); допуск перпендикулярности оси поверхности £ относительно поверхности А 0,1 мм в продольном направлении, 0,2 мм в поперечном направлении (рис. 5.57, п).

Торцевое биение - разность Д наибольшего и наименьшего расстояний от точек реального профиля торцевой поверхности до плоскости, перпендикулярной базовой оси (рис. 5.57, р). (Торцевое биение определяется в сечении торцевой поверхности цилиндром заданного диаметра, соосным с базовой осью, а если диаметр не задан, то в сечении любого диаметра торцевой поверхности.) Графическое изображение допуска торцевого биения Т показано на рис. 5.57, с. Условное обозначение на чертеже: допуск торцевого биения поверхности Б относительно оси отверстия А 0,04 мм (рис. 5.57, т) допуск торцевого биения поверхности Б относительно оси поверхности А 0,1 мм на диаметре 50 мм (рис. 5.57, у).

Полное торцевое биение - разность Д наибольшего и наименьшего расстояний от точек всей торцевой поверхности до плоскости, перпендикулярной базовой оси (рис. 5.57, ф). Графическое изображение допуска полного торцевого биения 7*показано на рис. 5.57, х. Условное обозначение на чертеже: допуск полного торцевого биения поверхности Б относительно оси отверстия Л 0,1 мм (рис. 5.57, и).

Лекция № 4.

Отклонения формы и расположения поверхностей .

ГОСТ 2.308-79

При анализе точности геометрических параметров деталей различают номинальные и реальные поверхности, профили; номинальное и реальное расположение поверхностей и профилей. Номинальные поверхности, профили и расположения поверхностей определяются номинальными размерами: линейными и угловыми.

Реальные поверхности, профили и расположения поверхностей получаются в результате изготовления. Они всегда имеют отклонения от номинальных.

Допуски формы.

В основу формирования и количественной оценки отклонений формы поверхностей положен принцип прилегающих элементов .

Прилегающий элемент , это элемент соприкасающийся с реальной поверхностью и расположенный вне материала детали, так чтобы расстояние от него в наиболее удалённой точке реальной поверхности в пределах нормируемого участка имело бы минимальное значение.

Прилегающим элементом может быть: прямая, плоскость, окружность, цилиндр и т.п. (Рис. 1, 2).

1 - прилегающий элемент;

2 – реальная поверхность;

L - длина нормируемого участка;

Δ - отклонение формы, определяемое от прилегающего элемента по нормали к поверхности.

Т - допуск формы.

Рис 2. Рис. 1

Поле допуска - область в пространстве, ограниченная двумя эквидистантными поверхностями, отстоящими одна от другой на расстоянии равном допуску Т, который откладывается от прилегающего элемента в тело детали.

Количественное отклонение формы оценивают наибольшим расстоянием от точек реальной поверхности (профиля) до прилегающей поверхности (профиля) по нормали к последней (рис.2). Прилегающими поверхностями служат: рабочие поверхности рабочих плит, интерференционных стекол, лекальных линеек, калибров, контрольных оправок и т.п.

Допуском формы называется наибольшее допускаемое отклонение Δ (рис.2).

Отклонения формы поверхностей.

1. Отклонение от прямолинейности в плоскости – это наибольшее от точек реального профиля до прилегающей прямой. (Рис. 3а).

Рис. 3

Обозначение на чертеже:

Допуск прямолинейности 0,1мм на базовой длине 200мм

2. Допуск плоскостности - это наибольшее допускаемое расстояние () от точек реальной поверхности до прилегающей плоскости в пределах нормированного участка (Рис. 3б).

Обозначение на чертеже:

Допуск плоскостности (не более) 0,02мм на базовой поверхности 200 100 мм.

Методы контроля.

Замер неплоскостности с помощью поворотного плоскомера.
Рис 5а.

Рис 5б. Схема замера неплоскостности.

Контроль в схеме 6б

осуществляется на просвет или

с помощью щупа

(погрешность 1-3мкм)

Рис 6. Схемы замера непрямолинейности.

Контроль плоскостности осуществляют:

Методом «На краску» по количеству пятен в рамке размером 25 25мм

С помощью интерференционных пластин (для доведенных поверхностей до 120мм) (Рис 7).

При наложении пластины с небольшим наклоном на проверяемую поверхность детали прямоугольной формы возникают интерференционные полосы, а на поверхности круглой детали - интерференционные кольца.

При наблюдении в белом свете расстояние между полосами равно в = 0,3мкм (половине длины волны белого света).

Рис. 7.

Неплоскостность оценивается в долях интервала интерференционных полос. По картинке мкм. мкм

Допуск прямолинейности оси цилиндра 0,01мм (стрелка допуска формы упирается в стрелку размера 20f 7). (Рис 8)

Схема замера

Допуски прямолинейности поверхностей задаются на направляющие; плоскостности - для плоских торцевых поверхностей для обеспечения герметичности (плоскости разъема корпусных деталей); работающих при больших давлениях (торцевые распределители) и т.д.

Допуски прямолинейности осей – для длинных цилиндрических поверхностей (типа штоков), перемещающихся в горизонтальном направлении; цилиндрических направляющих; для деталей, собирающихся с ответными по нескольким поверхностям.

Допуски и отклонения формы цилиндрических поверхностей.

1. Допуск круглости - наиболее допускаемое отклонение от круглости наибольшее расстояние i от точек реальной поверхности до прилегающей окружности.

Поле допуска - область, ограниченная двумя концентрическими окружностями на плоскости перпендикулярной оси поверхности вращения.

Допуск круглости поверхности 0,01мм.

Кругломеры

Рис 9. Схемы замера отклонения от круглости.

Частными видами отклонений от круглости являются овальность и огранка (Рис10).

Овальность Огранка

Для разной огранки индикаторную головку устанавливают под углом (Рис.9б).

2. Допуски цилиндричности - это наибольшее допускаемое отклонение реального профиля от прилегающего цилиндра.

Складывается из отклонения от круглости (замер не менее чем в трех точках) и отклонения от прямолинейности оси.

3. Допуск профиля продольного сечения – это наибольшее допускаемое отклонение профиля или формы реальной поверхности от прилегающего профиля или поверхности (заданных чертежом) в плоскости, проходящей через ось поверхности.

Допуск профиля продольного сечения 0,02мм.
Частные виды отклонения профиля продольного сечения:

Конусность Бочкообразность Седлообразность

Рис 11. Отклонение профиля продольного сечения а, б, в, г и схемы замера д.

Допуски круглости и профиля продольного сечения задаются для обеспечения равномерного зазора в отдельных сечениях и по всей длине детали, например, в подшипниках скольжения, для деталей пары поршень-цилиндр, для золотниковых пар; цилиндричности для поверхностей, требующих полноты контакта деталей (соединяющихся по посадкам с натягом и переходным), а также для деталей большой протяженности типа «штоков».

Допуски расположения

Допуски расположения - это наибольшие допустимые отклонения реального расположения поверхности (профиля), оси, плоскости симметрии от его номинального расположения.

При оценке отклонений расположения отклонения формы (рассматриваемых поверхностей и базовых) должны быть исключены из рассмотрения (Рис 12). При этом реальные поверхности заменяют прилегающими, а за оси, плоскости симметрии принимают оси, плоскости симметрии и центры прилегающих элементов.

Допуски параллельности плоскостей - это наибольшая допускаемая разность наибольшего и наименьшего расстояний между прилегающими плоскостями в пределах нормируемого участка.

Для нормирования и измерения допусков и отклонений расположения вводятся базовые поверхности, оси, плоскости и т.д.Это поверхности, плоскости, оси и т.д., которые определяют положение детали при сборке (работе изделия) и относительно которых задаётся положение рассматриваемых элементов. Базовые элементы на

чертеже обозначаются знаком ; используются большие буквы русского алфавита.

Обозначение баз, разрезов (А-А) не должны дублироваться. Если базой является ось или плоскость симметрии знак ставится на продолжение размерной линии:

Допуск параллельности 0,01мм относительно базовой

поверхности А.

Допуск соосности поверхности в

диаметральном выражении 0,02мм

относительно базовой оси поверхности

В том случае если конструкторская, технологическая (определяющая положение детали при изготовлении) или измерительная (определяющая положение детали при измерении) не совпадают следует выполнить пересчет выполненных измерений.

Измерение отклонений от параллельных плоскостей.

(в двух точках на заданной длине поверхности)

Отклонение определяется как разность показаний головки на заданном интервале друг от друга (головки на «0» выставляются по эталону).

Допуск параллельности оси отверстия относительно базовой плоскости А на длине L.

Рис 14. (Схема замера)

Допуск параллельности осей.

Отклонение от параллельности осей в пространстве - геометрическая сумма отклонений от параллельности проекций осей в двух взаимно перпендикулярных плоскостях. Одна из этих плоскостей является общей плоскостью осей (т.е. проходит через одну ось и точку другой оси). Отклонение от параллельности в общей плоскости - отклонение от параллельности проекций осей на их общую плоскость. Перекос осей - отклонение от проекций осей на плоскость перпендикулярную к общей плоскости осей и проходящую через одну из осей.

Поле допуска - это прямоугольный параллелепипед со сторонами сечения - , боковые грани параллельны базовой оси. Или цилиндр

Рис 15. Схема замера

Допуск параллельности оси отверстия 20H7 относительно оси отверстия 30Н7.

Допуск соосности.

Отклонение от соосности относительно общей оси – это наибольшее расстояние между осью рассматриваемой поверхности вращения и общей осью двух или нескольких поверхностей.

Поле допуска соосности – это область в пространстве, ограниченная цилиндром, диаметр которого равен допуску соосности в диаметральном выражении (Ф = Т ) или удвоенному допуску соосности в радиусном выражении: R=T/2 (рис. 16)

Допуск соосности в радиусном выражении поверхностей и относительно общей оси отверстий А.

Рис 16. Поле допуска соосности и схема замера

(отклонение оси относительно базовой оси А-эксцентриситет); R-радиус первого отверстия (R+e) – расстояние до базовой оси в первом положении замера; (R-e) – расстояние до базовой оси во втором положении после поворота детали или индикатора на 180 градусов.

Индикатор регистрирует разность показаний (R+e)-(R-e)=2e=2 - отклонение от соосности в диаметральном выражении.

Допуск соосности шеек вала в диаметральном выражении 0,02мм (20мкм) относительно общей оси АБ. Валы такого типа устанавливаются (базируются) на опоры качения или скольжения. Базой является ось, проходящая через середины шеек вала (скрытая база).

Рис 17. Схема несоосности шеек вала.

Смещение осей шеек вала приводит к перекосу вала и нарушению эксплуатационных характеристик всего изделия в целом.

Рис 18. Схема замера несоосности шеек вала

Базирование производится на ножевые опоры, которые помещаются в средние сечения шеек валов. При замере отклонение получается в диаметральном выражении D Æ = 2e.

Отклонение от соосности относительно базовой поверхности определяют обычно измерением биения проверяемой поверхности в заданном сечении или крайних сечениях – при вращении детали вокруг базовой поверхности. Результат измерения зависит от некруглости поверхности (которая приблизительно в 4 раза меньше отклонения от соосности).

Рис 19. Схема замера соосности двух отверстий

Точность зависит от точности пригонки оправок к отверстию.

Замер зависимого допуска можно производить с помощью калибра (рис. 20).

Допуск соосности поверхности относительно базовой оси поверхности в диаметральном выражении 0,02мм, допуск зависимый.

Допуск симметричности

Допуск симметричности относительно базовой плоскости – наибольшее допускаемое расстояние между рассматриваемой плоскостью симметрии поверхности и базовой плоскостью симметрии.

Рис 21. Допуски симметричности, схемы замера

Допуск симметричности в радиусном выражении 0,01мм относительно базовой плоскости симметрии А (рис. 21б).

Отклонение DR (в радиусном выражении)равно полуразности расстояний А и Б.

В диаметральном выражении DТ = 2e = А-Б.

Допуски соосности и симметричности назначаются на те поверхности, которые отвечают за точную собираемость и функционирование изделия, где не допускается значительных смещений осей и плоскостей симметрии.

Допуск пересечения осей.

Допуск пересечения осей – наибольшее допускаемое расстояние между рассматриваемой и базовой осями. Он определяется для осей, которые при номинальном расположении должны пересекаться. Допуск задается в диаметральном или радиусном выражении (рис. 22а).

Положение плоскости в пространстве определяется:

• тремя точками, не лежащими на одной прямой;
• прямой и точкой, взятой вне прямой;
• двумя пересекающимися прямыми;
• двумя параллельными прямыми;
• плоской фигурой.

В соответствии с этим на эпюре плоскость может быть задана:

• проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
• проекциями точки и прямой (Рисунок 3.1,б);
• проекциями двух пересекающихся прямых (Рисунок 3.1,в);
• проекциями двух параллельных прямых (Рисунок 3.1,г);
• плоской фигурой (Рисунок 3.1,д);
• следами плоскости;
• линией наибольшего ската плоскости.

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

Плоскость общего положения может иметь три следа: горизонтальный – απ 1 , фронтальный – απ 2 и профильный – απ 3 , которые она образует при пересечении с известными плоскостями проекций: горизонтальной π 1 , фронтальной π 2 и профильной π 3 (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А , В , С ; линии АС , АВ , ВС ; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций .

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями .

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

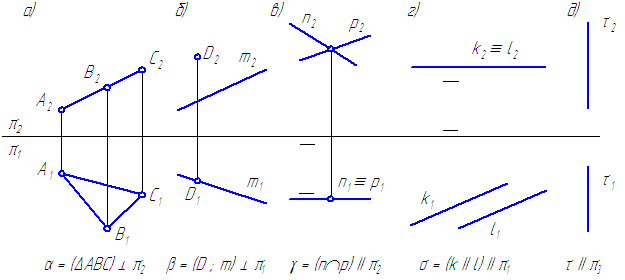
Рисунок 3.4 – Эпюры плоскостей частного положения

3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5).

Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости

α = m // n

D ∈ n ⇒ D ∈ α

Рисунок 3.6 – Принадлежность прямой плоскости

Упражнение

Дана плоскость, заданная четырехугольником (Рисунок 3.7, а). Необходимо достроить горизонтальную проекцию вершины С .

а	б

Рисунок 3.7 – Решение задачи

Решение :

1. ABCD – плоский четырехугольник, задающий плоскость.
2. Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
3. Согласно признаку пересекающихся прямых, построим горизонтальную проекцию точки пересечения этих прямых — K по её известной фронтальной проекции: A 2 C 2 ∩ B 2 D 2 =K 2 .
4. Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD : на проекции диагонали B 1 D 1 строим К 1 .
5. Через А 1 К 1 проводим проекцию диагонали А 1 С 1 .
6. Точку С 1 получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А 1 К 1 .

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π 1) (Рисунок 3.8, а; 3.9).

Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π 2) (Рисунок 3.8, б; 3.10).

Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π 3) (Рисунок 3.8, в; 3.11).

Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

Рисунок 3.12 – Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

1. Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
2. Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
3. Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN .

Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Упражнение

Заданы: прямая АВ общего положения, плоскость σ⊥π 1 . (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Решение :

1. Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ 1 (горизонтальный след плоскости);
2. Точка К должна принадлежать прямой АВ ⇒ К 1 ∈А 1 В 1 и заданной плоскости σ ⇒ К 1 ∈σ 1 , следовательно, К 1 находится в точке пересечения проекций А 1 В 1 и σ 1 ;
3. Фронтальную проекцию точки К находим посредством линии проекционной связи: К 2 ∈А 2 В 2 .

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Упражнение

Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.

а	б

Рисунок 3.15 – Пересечение прямой с плоскостью

1. Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
2. Если α⊥π 1 , то на плоскость проекций π 1 плоскость α проецируется в прямую (горизонтальный след плоскости απ 1 или α 1), совпадающую с E 1 F 1 ;
3. Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено );
4. Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K .

Алгоритм решения задачи (Рисунок 3.15, б):

Через EF проведем вспомогательную плоскость α:

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π 1 или π 2 .

Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций .

Необходимо отдельно определить видимость на каждой плоскости проекций.

Видимость на π 2 (рис. 3.15)

Выберем точки, конкурирующие на π 2 – точки 3 и 4. Пусть точка 3∈ВС∈σ , точка 4∈EF .

Чтобы определить видимость точек на плоскости проекций π 2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π 2 .

Направление взгляда на π 2 показано стрелкой.

По горизонтальным проекциям точек 3 и 4, при взгляде на π 2 , видно, что точка 4 1 располагается ближе к наблюдателю, чем 3 1 .

4 1 ∈E 1 F 1 ⇒ 4∈EF ⇒ на π 2 будет видима точка 4, лежащая на прямой EF , следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K

Видимость на π 1

Для определения видимости выберем точки, конкурирующие на π 1 – точки 2 и 5.

Чтобы определить видимость точек на плоскости проекций π 1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π 1 .

Направление взгляда на π 1 показано стрелкой.

По фронтальным проекциям точек 2 и 5, при взгляде на π 1 , видно, что точка 2 2 располагается ближе к наблюдателю, чем 5 2 .

2 1 ∈А 2 В 2 ⇒ 2∈АВ ⇒ на π 1 будет видима точка 2, лежащая на прямой АВ , следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.

Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

а	б

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K .

1. Построим горизонталь и фронталь в плоскости σ=ΔАВС : A-1 ∈σ; A-1 //π 1 ; С-2 ∈σ; С-2 //π 2 .
2. Восстановим из точки K перпендикуляр к заданной плоскости: p 1 ⊥h 1 и p 2 ⊥f 2 , или p 1 ⊥απ 1 и p 2 ⊥απ 2

3.8. Взаимное положение двух плоскостей

3.8.1. Параллельность плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Упражнение

Задана плоскость общего положения α=ΔАВС и точка F ∉α (Рисунок 3.17).

Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной

Решение :

В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.

1. Через точку F проводим прямую m , параллельную, например, АВ .
2. Через точку F , или же через любую точку, принадлежащую m , проводим прямую n , параллельную, например, ВС , причём m∩ n=F .
3. β = m ∩n и β//α по определению.

3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Упражнение

Две плоскости α и β заданы следами (Рисунок 3.18). Построить линию пересечения плоскостей.

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами

Порядок построения линии пересечения плоскостей :

1. Найти точку пересечения горизонтальных следов — это точка М (её проекции М 1 и М 2 , при этом М 1 =М , т.к. М – точка частного положения, принадлежащая плоскости π 1).
2. Найти точку пересечения фронтальных следов — это точка N (её проекции N 1 и N 2 , при этом N 2 = N , т.к. N – точка частного положения, принадлежащая плоскости π 2).
3. Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М 1 N 1 и М 2 N 2 .

М N – линия пересечения плоскостей.

Упражнение

Задана плоскость σ = ΔАВС , плоскость α – горизонтально- проецирующая (α⊥π 1) ⇒α 1 – горизонтальный след плоскости (Рисунок 3.19).

Построить линию пересечения этих плоскостей.

Решение :

Так как плоскость α пересекает стороны АВ и АС треугольника АВС , то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.

Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L , то есть K 1 и L 1 , на пересечении горизонтального следа (α 1) заданной плоскости α с горизонтальными проекциями сторон ΔАВС : А 1 В 1 и A 1 C 1 . После чего посредством линий проекционной связи находим фронтальные проекции этих точек K 2 и L 2 на фронтальных проекциях прямых АВ и АС . Соединим одноимённые проекции: K 1 и L 1 ; K 2 и L 2 . Линия пересечения заданных плоскостей построена.

Алгоритм решения задачи :

KL – линия пересечения ΔАВС и σ (α∩σ = KL ).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения

Упражнение

Заданы плоскости α = m//n и плоскость β = ΔАВС (Рисунок 3.20).

Построить линию пересечения заданных плоскостей.

Решение :

1. Чтобы найти точки, общие для обеих заданных плоскостей и задающие линию пересечения плоскостей α и β, необходимо воспользоваться вспомогательными плоскостями частного положения.
2. В качестве таких плоскостей выберем две вспомогательные плоскости частного положения, например: σ // τ; σ⊥π 2 ; τ⊥π 2 .
3. Вновь введённые плоскости пересекаются с каждой из заданных плоскостей α и β по прямым, параллельным друг другу, так как σ // τ:

— результатом пересечения плоскостей α, σ и τ являются прямые (4-5) и (6-7);

— результатом пересечения плоскостей β, σ и τ являются прямые (3-2) и (1-8).

1. Прямые (4-5) и (3-2) лежат в плоскости σ; точка их пересечения М одновременно лежит в плоскостях α и β, то есть на прямой пересечения этих плоскостей;
2. Аналогично находим точку N , общую для плоскостей α и β.
3. Соединив точки M и N , построим прямую пересечения плоскостей α и β.

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)

Алгоритм решения задачи :

Упражнение

Заданы плоскости α = ΔАВС и β = a //b . Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей

Решение :

Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π 2 , заключив прямую a во вспомогательную плоскость σ (σ∈a ). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а . Следовательно (1-2)∩а =K .

Точка К принадлежит обеим плоскостям α и β.

Следовательно, точка K , является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β.

Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π 2 (τ∈b ).

Соединив точки K и L , получим прямую пересечения плоскостей α и β.

3.8.3. Взаимно перпендикулярные плоскости

Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Упражнение

Задана плоскость σ⊥π 2 и прямая общего положения – DE (Рисунок 3.22)

Требуется построить через DE плоскость τ⊥σ.

Решение .

Проведём перпендикуляр CD к плоскости σ – C 2 D 2 ⊥σ 2 (на основании ).

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C 1 D 1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩ DE задают плоскость τ. Итак, τ⊥σ.

Аналогичные рассуждения, в случае плоскости общего положения.

Упражнение

Задана плоскость α = ΔАВС и точка K вне плоскости α.

Требуется построить плоскость β⊥α, проходящую через точку K .

Алгоритм решения (Рисунок 3.23):

1. Построим горизонталь h и фронталь f в заданной плоскости α = ΔАВС ;
2. Через точку K проведём перпендикуляр b к плоскости α (по теореме о перпендикуляре к плоскости : если прямая перпендикулярна плоскости, то её проекции перпендикулярны к наклонным проекциям горизонтали и фронтали, лежащих в плоскости: b 2 ⊥f 2 ; b 1 ⊥h 1 ;
3. Задаём плоскость β любым способом, например, β = a∩ b , таким образом, плоскость, перпендикулярная к заданной, построена: α⊥β.

Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС

3.9. Задачи для самостоятельного решения

1. Задана плоскость α = m //n (Рисунок 3.24). Известно, что K ∈α.

Постройте фронтальную проекцию точки К .

Рисунок 3.24

2. Постройте следы прямой, заданной отрезком CB , и определите квадранты, через которые она проходит (Рисунок 3.25).

Рисунок 3.25

3. Постройте проекции квадрата, принадлежащего плоскости α⊥π 2 , если его диагональ MN //π 2 (Рисунок 3.26).

Рисунок 3.26

4. Построить прямоугольник ABCD с большей стороной ВС на прямой m , исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

Рисунок 3.27

5. Задана плоскость α=a //b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

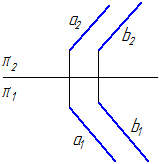
Рисунок 3.28

6. Задана плоскость α=∆АВС и точка D D плоскость β⊥α и β⊥π 1 .

7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE //α и DE //π 1 .

Любая технологическая операция может быть выполнена с определенной точностью, а значит размеры полученной в результате обработки детали не будут идеальными, они могут колебаться в некотором диапазоне. Для того, чтобы выполнить условия собираемости и обеспечить надежную работу детали в заданных условиях необходимо задать допустимый интервал, в который должен попасть итоговый размер. Этот интервал может регламентировать не только линейные или диаметральные размеры, но и форму или взаимное расположение поверхностей.

Допуски формы и расположения назначаются конструктором исходя из условий сборки и особенностей работы детали в механизме.

Виды допусков формы

Допуском формы называют максимальное допускаемое значение отклонения формы.

Поле допуска формы - это область на плоскости или в пространстве, внутри которой должны находиться все точки рассматриваемого элемента в пределах нормируемого участка, ширина или диаметр которой определяется значением допуска, а расположение относительно реального элемента прилегающим элементом.

Отклонения и допуски формы

Различают следующие допуски на отклонения формы:

• Отклонение от прямолинейности в плоскости
• выпуклость
• вогнутость
• Отклонение от плоскости и допус плоскостности
• Выпуклость
• Вогнутость
• Отклонение от круглости и допуск круглости
• Овальность
• Огранка
• Отклонение от цилиндричности и допуск цилиндричности
• Отклонение и допуск профиля продольного сечения цилиндрической поверхности
• Отклонение профиля продольного сечения
• Конусообразность
• Бочкообразность
• Седлообразность

Допустимые отклонения обозначаются специальными символами.

Виды допусков расположения

Допуск расположения - предел, ограничивающий допускаемое значение отклонения расположения.

Различают допуски месторасположения и допуски ориентации.

Поле допуска расположения - область на плоскости или в пространстве, внутри которой должен находиться прилегающий элемент или плоскость симметрии, ось, центр в пределах нормируемого участка, диаметр или ширина которой определяется значение допуска, а расположение относительно - номинальным расположением рассматриваемого элемента.

Отклонения и допуски расположения

Различают следующие виды допусков расположения:

• Отклонение от параллельности и допуск параллельности
• Отклонение и допуск перпендикулярности
• Отклонение и допуск наклона
• Отклонение и допуск соосности
• Допуск в радиусном выражении
• Отклонение и допуск симметричности
• Позиционное отклонение и позиционный допуск
• Допуск в диаметральном выражении
• Допуск в радиусном выражении
• Отклонение от пересечения и допуск пересечения осей
• Допуск в диаметральном выражении
• Допуск в радиусном выражении

Суммарные допуски

Существует несколько видов суммарных допусков формы и расположения.

• Радиальное биение
• Полное радиальное биение
• Торцовое биение
• Полное торцовое биение
• Биение в заданном направлении
• Отклонение и допуск формы заданного профиля
• Отклонение и допуск формы заданной поверхности

Эти допуски обозначаются символами.

Обозначение допусков формы и расположения на чертежах

Допуски формы и расположения изображают на чертежах в виде рамки, которая поделена на несколько частей. В первой части изображают графическое обозначение допуска, во второй части - числовое значение допуска, в третей и последующий - буквенное обозначение одной или нескольких баз.

В случае отсутствия базы допуска рамка состоит только из двух частей. Примеры рамок допусков формы и расположения показаны на рисунке.

На рисунке слева показана рамка с допуском формы (допустимое отклонение от прямолинейности), справа с допуском расположения (допустимое отклонение от параллельности).

Рамку выполняют тонкими линиями. Высота текста в рамке должна равняться размеру шрифта размерных чисел. От рамки допуска до поверхности или до выноски проводится линия, оканчивающаяся стрелкой.

Перед числовым значение допуска могут указываться знаки:

• ф - если цилиндрическое или круговое поле допуска указываются диаметром
• R - если цилиндрическое или круговое поле указываются радиусом
• Т - если поле допуска пересечения осей, симметричности, ограничены двумя параллельными прямыми или плоскостями в диаметральном выражении.
• Т/2 - в том же случае, что и Т, только в радиусном выражении
• Сфера - для шарового поля допуска.

Если допуск должен применяться не ко всей поверхности, а только к некоторому участку, то он обозначается штрих пунктирной линией.

Для одного элемента может быть указано несколько допусков, этом случае рамки изображаются одна над другой.

Дополнительная информация может быть указана над рамкой или под ней.

Информация о допусках формы и расположения может быть указана в .

Неуказанные допуски соосности по ГОСТ 25069-81.

Зависимые допуски

Зависимые допуски расположения обозначают следующим символом .

Этот символ может быть размещен после числового значения допуска, если зависимый допуск связан с действительными размерами рассматриваемого элемента. Также символ может быть размещен после буквенного обозначение (если оно отсутствует то в третьем поле рамки) в том случае, если зависимый допуск связан с действительными размерами базового элемента.

Назначение допусков формы и расположения

Чем точнее изготовлена деталь, тем более точные инструменты потребуются для ее изготовления и контроля размеров. Это автоматически увеличит ее стоимость. Получается, что цена изготовления детали во многом зависит от требуемой точности при ее изготовлении. Это означает, что конструктор должен указать лишь те допуски, которые действительно необходимы для сборки и надежной работы механизма. Допустимые интервалы также должны быть назначены исходя из условий собираемости и работоспособности.

Числовые значения допусков формы

В зависимости от класса точности устанавливаются стандартные значения допусков формы.

Допуски плоскостности и прямолинейности

Номинальным размеров в данном случае считается номинальная длина нормированного участка.

Допуски круглости, цилиндричности, профиля продольного сечения

Данные допуски назначаются в тех случаях, когда они должны быть меньше, чем допуск размера.

Номинальным размером считается номинальный диаметр поверхности.

Допуски перпендикулярности, параллельности, наклона, торцевого биения

Номинальным размером при назначении допусков на параллельность, перпендикулярность, наклон понимается номинальная нормируемого участка или номинальная длина всей контролируемой поверхности.

Допуски радиального биения, симметричности, соосности пересечения осей в диаметральном выражении

При назначении допусков радиального биения номинальным размером считается номинальный диаметр рассматриваемой поверхности.

В случае назначения допусков симметричности, пересечения осе соосности номинальным размером считается номинальный диаметр поверхности или номинальный размер между поверхностями, которые образуют рассматриваемый элемент.

Параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Доказательство. Пусть a и b - данные плоскости, а 1 и а 2 – прямые в плоскости a , пересекающиеся в точке А , b 1 и b 2 соответственно параллельные им прямые в плоскости b . Допустим, что плоскости a и b не параллельны, то есть они пересекаются по некоторой прямой с . Прямая а 1 параллельна прямой b 1 , значит она параллельна и самой плоскости b (признак параллельности прямой и плоскости). Прямая а 2 параллельна прямой b 2 , значит она параллельна и самой плоскости b (признак параллельности прямой и плоскости). Прямая с принадлежит плоскости a , значит хотя бы одна из прямых а 1 или а 2 пересекает прямую с, то есть имеет с ней общую точку. Но прямая с также принадлежит и плоскости b , значит, пересекая прямую с, прямая а 1 или а 2 пересекает плоскость b , чего быть не может, так как прямые а 1 и а 2 параллельны плоскости b . Из этого следует, что плоскости a и b не пересекаются, то есть они параллельны.

Теорема 1 . Если две параллельные плоскости пересекаются третей, то прямые пересечения параллельны.
Доказательство. Пусть a и b - параллельные плоскости, а g - плоскость, пересекающая их. Плоскость a пересеклась с плоскостью g по прямой а. Плоскость b пересеклась с плоскостью g по прямой b . Линии пересечения а и b лежатв одной плоскости g и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.

Теорема 2. Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.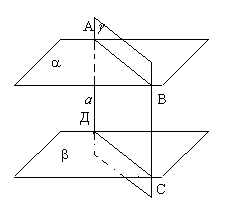
Доказательство. Пусть a и b - параллельные плоскости, а а и b – параллельные прямые, пересекающие их. Через прямые а и b проведем плоскость g (эти прямые параллельны, значит определяют плоскость, причем только одну). Плоскость a пересеклась с плоскостью g по прямой АВ. Плоскость b пересеклась с плоскостью g по прямой СД.По предыдущей теореме прямая с параллельна прямой d . Прямые а, b , АВ и СД принадлежат плоскости g .Четырехугольник, ограниченный этими прямыми,есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть АД = ВС